|
The Cell |
|
The Cell |
How Permanent Magnets Could Alter the Cell Membrane
Permanent magnets are enthusiastically recommended for pain relief by millions of people around the world. Yet, many in the scientific establishment are skeptical of these claims. Why? A major factor is the absence of a mechanism that fits current medical models. For instance, as discussed in the previous section on Lorentz forces, static magnetic effects on blood flow are thousands of times too small to make any difference to our well being. With such facts, skepticism logically follows. It is the purpose of this article to propose a magnetic mechanism that is robust enough to affect pain sensors. It is not necessary that the mechanism actually accounts for magnetic pain relief, only that it could. Hopefully, this will soften the skepticism and encourage further research until biomagnetic phenomena are fully understood.
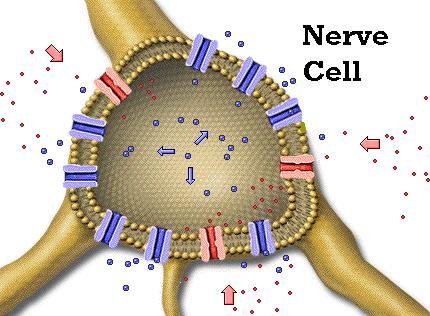 Cells in the human
body are surrounded by fatty molecules that form a thin membrane. The
cell
membrane keeps cell machinery inside and body fluids outside. The
concentration
of chemicals inside a cell differs greatly from the fluid outside. Of
particular
importance are the three ions of potassium, sodium and chlorine (
K+, Na+, Cl- ). Ions are atoms that
have
lost or gained electrons making them electrically charged. Potassium
ions
are concentrated inside cells, while sodium and chlorine ions dominate
on
the outside. This creates a voltage difference across the cell membrane
on
the order of -60 to -80 millivolts, abbreviated mV. ( A flashlight
battery
produces 1.5 volts or 1500 mV to give you an idea of scale.)
Pain
sensors are specialized nerve cells that send out electrical signals
when
the cell membrane voltage is locally reduced by about 20 mV. In other
words,
if someone pokes you with a pin and this causes the -70 mV membrane
voltage
of a nerve cell to drop to -50 mV, you say ouch!
Cells in the human
body are surrounded by fatty molecules that form a thin membrane. The
cell
membrane keeps cell machinery inside and body fluids outside. The
concentration
of chemicals inside a cell differs greatly from the fluid outside. Of
particular
importance are the three ions of potassium, sodium and chlorine (
K+, Na+, Cl- ). Ions are atoms that
have
lost or gained electrons making them electrically charged. Potassium
ions
are concentrated inside cells, while sodium and chlorine ions dominate
on
the outside. This creates a voltage difference across the cell membrane
on
the order of -60 to -80 millivolts, abbreviated mV. ( A flashlight
battery
produces 1.5 volts or 1500 mV to give you an idea of scale.)
Pain
sensors are specialized nerve cells that send out electrical signals
when
the cell membrane voltage is locally reduced by about 20 mV. In other
words,
if someone pokes you with a pin and this causes the -70 mV membrane
voltage
of a nerve cell to drop to -50 mV, you say ouch!
The Nernst Equilibrium:
Cell equilibrium is maintained by pumps and tiny holes in the membrane called pores. The pumps force unequal concentrations and the pores allow ion flow to balance electrical charge. The balance conditions can be calculated by considering two pore processes: diffusion and electrical pressure. When you drop food color into water, it spreads from a spot of intense color to larger volumes of lighter color. At the start, the color spreads rapidly because it is concentrated. As the concentration drops, the changes occur more slowly. This process is called diffusion and the color currents are proportional to concentration differences, called concentration gradients. The same thing happens to ions with concentration differences between the inside and outside of a cell. Ion current may then be described by a simple formula, current is proportional to the concentration gradient. The constant in the equation is negative because the current flows away from the point of highest concentration.
Diffusion Current = Jdiffusion = -(Constant) x (Concentration Gradient)
The diffusion current is powered by the random motion of atoms as they wiggle and bounce off one another due to their heat energy. The situation is somewhat similar for electrical forces. Charged particles of the same ion repel one another electrostatically. When concentrated, they tend to get pushed to areas of lower concentration. The work done to concentrate these ions is known as voltage. The difference in voltage between regions is described as a voltage gradient. If you think this sounds a lot like the case of diffusion, you are right. So, the formulas are quite similar.
Electric Current = Jelectric = -(Constant) x (Voltage Gradient)
These processes tend to push ions around until forces are balanced. Equilibrium occurs when the sum of currents equals zero. When each ion is considered separately, the Nernst Equation results, named after Walther Nernst in 1888. It calculates the difference in voltage across the cell membrane that achieves balance. His equation is shown below along with a table of values for typical concentrations of potassium, sodium and chlorine appropriate for mammals.
Jion = Jdiffusion + Jelectric = 0
VNernst = -(RT/zF) x ln (c/C)
z = valence = +/- 1
ln = Natural Log Function
R = Gas Constant = 8.314 J/mol.K
F = Faraday's Constant = 9.649x104 C/mol
T = Body Temperature in Kelvin = 37 + 273 = 310 K
c/C = Ratio of Ion Concentration Inside Cell to Outside Cell
p = Relative Permeability of Ion (not used until next section below)
| Name |
Ion |
p |
c |
C |
c/C |
ln(c/C) |
VNernst |
| Potassium |
K+ |
1.0 | 125 |
5 |
25.0 | 3.219 | -86.0 mV |
| Sodium |
Na+ |
0.1 |
12 |
120 | 0.10 | -2.303 | +61.5 mV |
| Chlorine |
Cl- |
0.6 |
5 |
125 | 0.04 | -3.219 | -86.0 mV |
The Goldman-Hodgkin-Katz Equation:
The Nernst equilibrium applies only to solutions with a single type of ion. Sixty years later, Goldman, Hodgkin and Katz extended the work of Nernst to include mixtures of ions. For a three ion mixture that models the human body, the total current across a membrane must include both diffusion and electric currents for potassium, sodium and chlorine ions. The sum of these currents must be zero for the cell to be in balance. The equations for zero sum current and the resulting membrane voltage calculation are given below. Note that "membrane potential" is a synonym for "membrane voltage" and the two are used interchangeably.
Jtotal = JK + JNa+ JCl = 0
VMembrane = -(RT/F) x ln [ (pc1+pc2+pC3) / (pC1+pC2+pc3) ]
pc = permeability times concentration inside
cell
pC = permeability times concentration outside cell
for ions of K=1, Na=2 and Cl=3
Note that pc1 and pc2 terms (concentrations inside the cell) are in the numerator of the natural log for positive ions K+ and Na+. However, for negative ion Cl-, the pc3 term is in the denominator. This is due to the sign inversion of the valence term in the original Nernst equation. For the typical mammalian values given in the table above, the membrane potential becomes:
VMembrane = -0.02672 x ln [
(1x125+0.1x12+0.6x125)
/ (1x5+0.1x120+0.6x5) ] mV
VMembrane ( K,Na,Cl mixture in a
mammalian
cell ) = -61.7 mV
Lorentz Forces Within the Cell Membrane:
As you may recall, a Lorentz force pushes an ion sideways as it speeds through the magnetic field of a permanent magnet. Lorentz force is equal to ion charge x ion speed x magnet strength, so the faster an ion travels, the more the sideways push. Within a cell membrane pore, the electric field gradient is intense because the wall is so thin. Perhaps, this could accelerate ions to high enough speeds for Lorentz forces to be meaningful. The highest possible speed would be achieved by an ion that shot through the cell pore without bumping into any other particles. This would be an upper limit for the speed of any particular ion. Such an upper limit is calculated below. Note that the driving voltage is due to the mismatch between the Nernst and actual membrane potentials. If there is no mismatch, the current is zero so the average ion speed must be zero. If the Nernst and membrane potentials are of opposite sign, the mismatch is greater and so will be the speed of the ions.
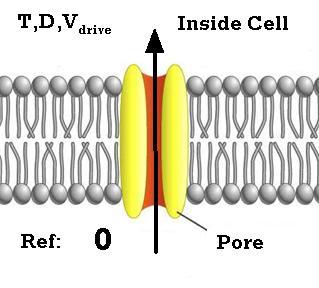
| formulas |
d = st |
F = ma |
F = qE |
| variables |
t = time |
F = force |
q = charge |
| constants | T = transit time D = wall thickness S = average speed |
Vdrive = |
E = Vdrive / D |
Electrostatic Force = F = ma = qE = qVdrive / D
S = aT/2 = a/2 ( 2D/a )1/2 = ( aD/2 )1/2 = (
FD/2m
)1/2
Maximum Average Speed = S = [
qVdrive / 2m ] 1/2
The maximum average speed is calculated for all three ions with results
in
the table below. Note the speed of sodium ions may approach 500
meters/second.
This is 50,000 times faster than the speed we used to evaluate (and
then
dismiss) the Lorentz forces on blood flow in the previous section.
Clearly,
this is a case where Lorentz forces may be of some significance.
|
Ion |
VNernst |
Vdrive |
Mass |
Speed |
Perm |
kSB |
Perm |
|
K+ |
-86.0 mV | 24.3 mV | 64.91x10-27 |
172 |
1.0 |
0.1 |
.90 |
|
Na+ |
+61.5 mV |
123 mV |
38.16x10-27 |
508 |
0.1 |
0.3 |
.07 |
|
Cl- |
-86.0 mV |
24.3 mV |
58.85x10-27 |
178 |
0.6 |
0.1 |
.54 |
How would a magnetic field affect an ion traveling through a cell pore? A Lorentz force always operates at right angles to the direction of motion. Since ions are aligned by the electric field and shoot straight through the membrane pores, a Lorentz force would always push an ion off course. This would make it more likely to bump into the sides of the pore, decreasing the efficiency of the process. A measure of the ease with which ions penetrate the membrane is called permeability and is denoted by the symbol p in the equation for membrane voltage. As a first approximation, you might expect base permeability to be slightly reduced by both speed and magnetic field strength. A candidate might be the formula below where kSB is a number significantly less than 1 that varies with the average ion speed S and magnetic field strength B.
Permeability (magnetic) = pmag = pbase ( 1 - kSB )
The base permeability for our three ions is included in the above table along with a trial estimate for kSB to yield a final set of permeabilities that conform to expected ion speeds. Using these reduced permeabilities results in an altered membrane potential for typical mammal cells. The new membrane voltage is -65.4 mV which is 3.7 mV more negative than the old membrane voltage. Now, 3.7 mV doesn't sound like much. But, it gets added to the 20 mV threshold voltage which needs to be breached for a stimulus to activate a nerve sensor and cause pain. This represents an 18.5% increase in the pain threshold, just about what all those advocates of magnets are yelling about.
Vmag = -0.02672 ln
[ (.9x125+.07x12+.54x125)
/ (.9x5+.07x120+.54x5) ] mV
Lorentz Force Altered Membrane Potential = Vmag
= -65.4 mV
Threshold Increase = 100%(Vmem-Vmag)/20mV
=
18.5%
All of these calculations of membrane potential are based on the recognized science of our day as presented in the wonderful book, Bioelectricmagnetism by Malmivuo and Plonsey which is available online. My assumption that a Lorentz force would decrease ion permeability in proportion to speed seems reasonable. Where the argument gets weak is the assignment of a 30% reduction in sodium permeability along with 10% reductions for potassium and chlorine. These are numbers picked out of the air. They could just as easily be 3% and 1% resulting in a much smaller increase in the stimulus threshold. Whether or not this is the actual mechanism of magnetic pain relief is not important. The simple realization that a possible mechanism exists is the real message. Static magnetic fields can become players at the ionic speeds of our nervous system. Perhaps, it's time for the skeptics to take a step backwards and think more deeply before they speak.
|
Rybett Controls Free Information Websites |